Choosing a classification algorithm
Five main steps involved in training a machine learning algorithm:
- Selection of features.
- Choosing a performance metric.
- Choosing a classifier and optimization algorithm.
- Evaluating the performance of the model.
- Tuning the algorithm.
Training a perceptron via scikit-learn
We train a perceptron model similar to CH2 and again use the Iris dataset. This time, however, we do it with the help of scikit-learn.
from sklearn import datasets
import numpy as np
# __________ Obtain desired feautures/labels from the iris dataset. __________
iris = datasets.load_iris()
# Assign sample features (1) petal length and (2) petal width to X.
X = iris.data[:, [2, 3]]
# Flower names stored as integers:
# Setosa(0), Versicolor(1), Virginica(2).
y = iris.target
# _________ Split dataset into separate training and test datasets. _________
from sklearn.cross_validation import train_test_split
# Randomly split X and y arrays to 30% test data, 70% training data.
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0)
# __________ Feature scaling: standardize features using StandardScaler class. __________
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
# Estimate training data mean and stdDev for each feature dimension.
sc.fit(X_train)
# Standardize both training and test data using the found values of mu, sigma.
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
# __________ Train a perceptron model. __________
from sklearn.linear_model import Perceptron
ppn = Perceptron(n_iter=40, eta0=0.1, random_state=0)
ppn.fit(X_train_std, y_train)
# __________ Make predictions on the test data. __________
from sklearn.metrics import accuracy_score
y_pred = ppn.predict(X_test_std) # Test data consists of 45 samples.
print('Misclassified samples: %d' % (y_test != y_pred).sum())
print('Accuracy: %.2f' % accuracy_score(y_test, y_pred)) # = 1 - 4/45 = 0.91
Misclassified samples: 4
Accuracy: 0.91
%matplotlib inline
# Modify plot_decision_regions function from CH2 and plot (some comments from ch2 omitted)
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
# Setup marker generator and color map.
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# Plot the decision surface.
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# Plot all samples.
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
alpha=0.8, c=cmap(idx),
marker=markers[idx], label=cl)
# NEW:
# Highlight test samples.
if test_idx:
X_test, y_test = X[test_idx, :], y[test_idx]
plt.scatter(X_test[:, 0], X_test[:, 1], c='',
alpha=1.0, linewidths=1, marker='o',
s=55, label='test set')
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))
plot_decision_regions(X=X_combined_std,
y=y_combined,
classifier=ppn,
test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.xlabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()
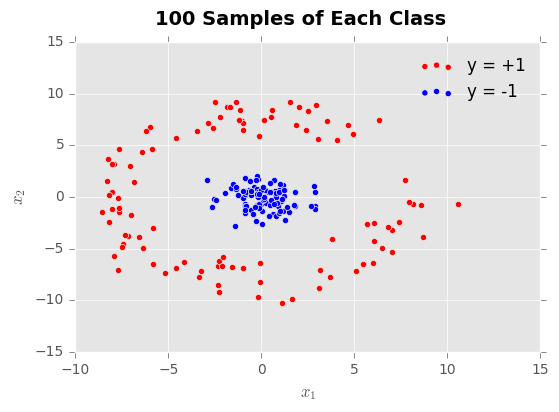
Modeling class probabilities via logistic regression
- Biggest disadvantage of perceptron: never converges if classes are not perfectly linearly separable.
- More powerful algorithm for linear and binary classification is logistic regression (not actually regression; is classification).
Logistic regression intuition and conditional probabilities
- odds ratio: the odds in favor of a particular event, $\frac{p}{1-p}$.
- $p$ refers to the probability of the positive event which we just define as the outcome we want to predict.
- The logit function, defined as the logarithm of the odds ratio:
- Input: values in the range 0 to 1 (probabilities of a class, given a particular sample).
- Output: values over the entire real number range.
- We, however, want the inverse behavior of this; we want to know the probability of a class, given a sample, by inputting values in the real number range. This function is called the logistic function, abbreviated as sigmoid function: \(\phi(z) = \frac{1}{1 + e^{-z}}\)
- where $z = \mathbf{w}^T\mathbf{x}$.
- As $z \rightarrow \infty$, $\phi(z) \rightarrow 1$, and as $z \rightarrow -\infty$, $\phi(z) \rightarrow 0$.